Author:baiyucraft
BLog: baiyucraft’s Home
原文:《动手学深度学习》
线性神经网络:
在进行下一个模型的介绍前,先介绍几个常用的损失函数:
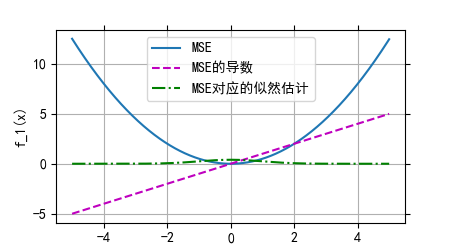
1.均方差损失(MSE)-L2 Loss
均方差损失是机器学习、深度学习回归任务中最常用的一种损失函数,也称为 L2 Loss。基本形式:
l=2N1i=1∑N(yi−yi)2
对于真实值 y=0 ,其预测值的均方差变化图、导数和对应似然函数的变化图如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| import numpy as np
x = np.arange(-5, 5, 0.01)
y_true = 0
def f_1(x):
return 1/2 * abs(x - y_true)**2
def f_1_d(x):
return x - y_true
def f_1_normal(x, mu=0, sigma=1):
return 1 / math.sqrt(2 * math.pi * sigma ** 2) * np.exp(-0.5 / sigma ** 2 * (x - mu) ** 2)
plot(x, [f_1(x), f_1_d(x), f_1_normal(x)], xlabel='x', ylabel='f_1(x)', figsize=(4.5, 2.5), legend=['MSE', 'MSE的导数', 'MSE对应的似然估计'])
|
运行结果:
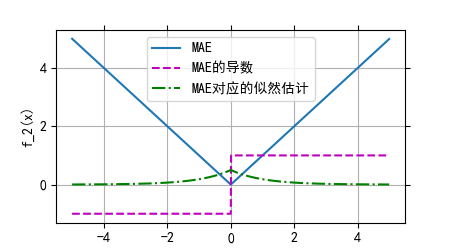
2.平均绝对误差(MAE)-L1 Loss
平均绝对误差是另一类常用的损失函数,基本形式:
l=N1i=1∑N∣yi−yi∣
对于真实值 y=0 ,其预测值的均方差变化图、导数和对应似然函数的变化图如下:
1
2
3
4
5
6
7
8
9
10
11
|
def f_2(x):
return abs(x - y_true)
def f_2_d(x):
return [-1 if x_i < 0 else 1 for x_i in x]
def f_2_lp(x, mu=0, la=1):
return 1 / (2*la) * np.exp(- abs(x-mu)/la)
plot(x, [f_2(x), f_2_d(x), f_2_lp(x)], xlabel='x', ylabel='f_2(x)', figsize=(4.5, 2.5),legend=['MAE', 'MAE的导数', 'MAE对应的似然估计'])
|
运行结果:
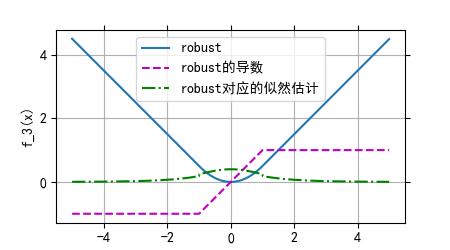
3.huber robust Loss
上文我们分别介绍了 MSE 和 MAE 损失以及各自的优缺点,MSE 损失收敛快但容易受 outlier 影响,MAE 对 outlier 更加健壮但是收敛慢,Huber Loss则是一种将 MSE 与 MAE 结合起来,取两者优点的损失函数,也被称作Smooth Mean Absolute Error Loss。其原理很简单,就是在误差接近 0 时使用 MSE,误差较大时使用 MAE,公式为:
l=⎩⎨⎧N1∑i=1Nδ∣yi−yi∣−21δ2,2N1∑i=1N(yi−yi)2,∣yi−yi∣>δ∣yi−yi∣≤δ
对于 δ=1 真实值 y=0 ,其预测值的均方差变化图、导数和对应似然函数的变化图如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
de = 1
def f_3(x):
return [de * abs(x_i - y_true) - 1 / 2 * de ** 2 if abs(x_i - y_true) > de else 1 / 2 * abs(x_i - y_true) ** 2 for
x_i in x]
def f_3_d(x):
res = []
for x_i in x:
if x_i < -de:
res.append(-1)
elif -de <= x_i < de:
res.append(x_i - y_true)
else:
res.append(1)
return res
def f_3_l(x, mu=0, la=1):
return [1 / (2 * la) * np.exp(- abs(x_i - mu) / la) if abs(x_i - y_true) > de else 1 / math.sqrt(
2 * math.pi * la ** 2) * np.exp(-0.5 / la ** 2 * (x_i - mu) ** 2) for x_i in x]
plot(x, [f_3(x), f_3_d(x), f_3_l(x)], xlabel='x', ylabel='f_3(x)', figsize=(4.5, 2.5), legend=['robust', 'robust的导数', 'robust对应的似然估计'])
|
运行结果: