D2L 7.线性回归的从零开始实现

Author：baiyucraft

前文：深度学习 6.线性回归概述 - baiyucraft’s Home
在了解线性回归的关键思想之后，我们可以开始通过代码来动手实现线性回归了。

1 2	`import random import torch`

1.生成数据集

我们首先根据带有噪声的线性模型构造一个人造的数据集，我们的任务是使用这个有限样本的数据集来恢复这个模型的参数。我们将使用低维数据，这样可以很容易地将其可视化。

我们使用预设的权重 $w = [2,-3.4]^{\mathrm{T}}$ 、 $b = 4.2$ 和噪声 $\epsilon$ 生成数据集的特征 $\boldsymbol{X}$ 及其目标 $\boldsymbol{y}$ ：

\boldsymbol{y} = \boldsymbol{Xw} + b + \epsilon

你可以将 $\epsilon$ 视为捕获特征和目标时的潜在观测误差。在这里我们认为标准假设成立，即 $\epsilon$ 服从均值为0的正态分布。为了简化问题，我们将 $\epsilon$ 的标准差设为0.01。

def synthetic_data(w, b, num_examples):
    """合成数据，生成 y = Xw + b + 噪声。"""
    # N(0,1)正态分布抽取 num_examples行 len(w)列 特征
    X = torch.normal(0, 1, (num_examples, len(w)))
    # 生成 num_examples 个随机数据
    y = torch.matmul(X, w) + b
    # 添加随机噪点
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape(-1, 1)

# 生成数据
true_w = torch.tensor([2, -3.4])
true_b = 4.2
# 生成数据集 特征 和 目标
features, targets = synthetic_data(true_w, true_b, 1000)
print('\n======features======\n', features)
print('\n======targets======\n', targets)

运行结果：

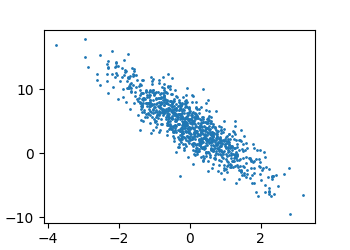
通过生成第二个特征 features[:, 1] 和 targets 的散点图，可以直观地观察到两者之间的线性关系：

# 查看生成数据集的分布
set_figsize()
# s=1 点的大小
plt.scatter(features[:, 1].numpy(), targets.numpy(), s=1)
plt.show()

运行结果：

2.读取数据集

这里定义一个data_iter 函数，该函数能打乱数据集中的样本并以小批量方式获取数据，这样就能使用小批量随机梯度下降：

def data_iter(batch_size, features, targets):
    """接收批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量"""
    num_examples = len(features)
    # 生成 0 - (num_examples-1) 的数列
    indices = list(range(num_examples))
    # 将数字打乱：这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)
    # 遍历数据
    for i in range(0, num_examples, batch_size):
        # 从打乱的 indices 中顺序取10个下标，并转换成 tensor
        batch_indices = indices[i:i + batch_size]
        # 返回
        yield features[batch_indices], targets[batch_indices]

3.定义模型

线性回归模型是 $\boldsymbol{y} = \boldsymbol{Xw} + b$ ，所以我们定义模型，这里 $b$ 是标量，所以运用了广播机制：

# 定义模型
def linreg(X, w, b):
    """线性回归模型。"""
    return torch.matmul(X, w) + b

4.定义损失函数

因为要更新模型。需要计算损失函数的梯度，这里采用的是平方损失函数：

1
2
3

def squared_loss(y_hat, y):
    """均方损失（平方误差）"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

5.定义优化算法

小批量随机梯度下降的工作示例：

在每一步中，使用从数据集中随机抽取的一个小批量，然后根据参数计算损失的梯度。接下来，朝着减少损失的方向更新我们的参数。下面的函数实现小批量随机梯度下降更新。该函数接受模型参数集合￥ $params$ (例如 $\boldsymbol w$ 、 $b$ )、学习速率 $lr$ 和批量大小 $batch\_size$ 作为输入。每一步更新的大小由 $lr$ 决定。因为我们计算的损失是一个批量样本的总和，所以我们用 $batch\_size$ 来归一化步长，这样步长大小就不会取决于我们对批量大小的选择，针对公式：

\boldsymbol{param} \gets \boldsymbol{param_{t-1}} - \dfrac{lr}{batch\_size} \sum_{i \in batch\_size}\dfrac{\partial}{\partial \boldsymbol{param_{t-1}}} l^{(i)}([params])

# 定义优化算法
def sgd(params, lr, batch_size):
    """小批量随机梯度下降。params（优化参数，例w、b），lr（学习率）"""
    with torch.no_grad():
        for param in params:
            # 优化
            param -= lr * param.grad / batch_size
            # 梯度归零
            param.grad.zero_()

6.训练

做好了前文中的定义，我们就可以开始训练了。训练过程是：

在每次迭代中，我们读取一小批量训练样本，并通过我们的模型来获得一组预测。计算完损失后，我们开始反向传播，存储每个参数的梯度。最后，我们调用优化算法 sgd 来更新模型参数。

具体执行是：

初始化参数 w 和 b
重复，直到完成
- 计算梯度 $g \gets \dfrac{\partial}{\partial (\boldsymbol{w},b)} l\left(\boldsymbol{x}^{(i)}, y^{(i)}, \boldsymbol{w},b\right)$
- 更新参数 $(\boldsymbol{w},b) \gets (\boldsymbol{w},b) - \dfrac{lr}{batch\_size} g$

在每个迭代周期epoch中，我们使用 data_iter 函数遍历整个数据集，并将训练数据集中所有样本都使用一次（假设样本数能够被批量大小整除）。这里的迭代周期个数num_epochs和学习率lr都是超参数，分别设为3和0.03。（设置超参数很棘手，需要通过反复试验进行调整。之后会讲解）。

因为我们使用的是自己合成的数据集，所以我们知道真正的参数是什么。因此，我们可以通过比较真实参数和通过训练学到的参数来评估训练的成功程度。事实上，真实参数和通过训练学到的参数确实非常接近。

# 初始化模型参数
# 随机生成 权重w 、偏置b=0 开始
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
batch_size = 10
# 学习率
lr = 0.03
# 数据扫3遍
num_epochs = 3
# 模型
net = linreg
# 损失
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, targets):
        # X 和 y 的小批量损失
        l = loss(net(X, w, b), y)
        # 因为 l 形状是(batch_size, 1)，而不是一个标量。l中的所有元素被加到一起，
        # 并以此计算关于[w, b]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), targets)
        print(f'epoch:{epoch + 1}, loss:{float(train_l.mean()):f}')

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

运行结果：

注意，我们不应该想当然地认为我们能够完美地恢复参数。在机器学习中，我们通常不太关心恢复真正的参数，而更关心那些能高度准确预测的参数。幸运的是，即使是在复杂的优化问题上，随机梯度下降通常也能找到非常好的解。其中一个原因是，在深度网络中存在许多参数组合能够实现高度精确的预测。

D2lLearning

#深度学习 #PyTorch #Python #线性神经网络

D2L 7.线性回归的从零开始实现

http://baiyucraft.top/D2lLearning/D2lLearning-7.html

作者

baiyucraft

发布于

2021年6月15日

许可协议

D2L 9.损失函数上一篇

D2L 8.线性回归的简洁实现下一篇