D2L 6.线性回归概述

Author：baiyucraft

BLog： baiyucraft’s Home

原文：《动手学深度学习》

  在机器学习中的大部分任务通常都是与预测有关的，当我们想预测一个数值时，就会涉及到回归问题。常见的例子有：预测价格（房屋、股票等）、预测住院时间（针对住院病人）、预测需求（零售销量）等。

一、线性回归的基本元素

  线性回归linear regression是回归的各种标准工具中最简单而且最流行的。线性回归基于几个简单的假设：首先，假设自变量 $\boldsymbol x$ 和因变量y之间的关系是线性的，即y可以表示为 $\boldsymbol x$ 中元素的加权和，这里通常允许包含观测值的一些噪声；其次，我们假设任何噪声都比较正常，如噪声遵循正态分布。

  这里举一个实际例子，我们希望根据房子的面积area和房龄age来估算房屋价格price。在这个过程中我们需要一个真实的数据集，这个数据集包括了房屋的销售价格、面积和房龄，在机器学习是术语中叫做训练集training set，每行数据称为样本sample，也可以称为数据点data point或数据样本data instance。我们要试图预测的目标（在这个例子中是房屋价格）称为标签label或目标target。预测所依据的自变量（面积和房龄）称为特征features或协变量covariates。

  通常，我们使用 $n$ 来表示数据集中的样本数。对索引为 $i$ 的样本，其输入表示为 $x^{(i)} = \left[x_1^{(i)}, x_2^{(i)}\right]^\mathrm{T}$，其对应的目标是 $y^{(i)}$。

1.线性模型

  我们需要先对该模型进行假设，即目标（房屋价格）可以表示特征（面积、房龄）的加权和，即：

$$price = w_{area} · area + w_{age} · age + b$$

  其中 $w_{area}$ 和 $w_{age}$ 都被称作权重weight，$b$ 被称作偏置bias，或称为偏移量offset、截距intercept。

  权重weight决定了每个特征对我们预测值的影响。偏置bias是指当所有特征都取值为0时，预测值应该为多少。即使现实中不会有任何房子的面积是0或房龄正好是0年，我们仍然需要偏置项。如果没有偏置项，我们模型的表达能力将受到限制。 严格来说，上述式子是输入特征的一个仿射变换affine transformation。仿射变换的特点是通过加权和对特征进行线性变换linear transformation，并通过偏置项来进行平移translation。

  同理类推，当我们的输入包含 $d$ 个特征时，我们将预测结果 $\widehat y$（通常使用 “尖角” 符号表示估计值）表示为：

$$\widehat y = w_1x_1 + \cdots + w_dx_d + b$$

  将所有特征放到 $\boldsymbol x \in \mathbb{R}^{d}$ 中，并将所有权重放到 $\boldsymbol w \in \mathbb{R}^{d}$ 中，我们就可以用点积形式来简洁地表达模型：

$$\widehat{y} = \boldsymbol w^\mathrm{T} \boldsymbol x + b$$

  向量 $\boldsymbol x$ 对应于单个数据样本的特征。用符号表示的矩阵 $\boldsymbol x \in \mathbb{R}^{n \times d}$ 可以很方便地引用我们整个数据集的 $n$ 个样本。其中， $\boldsymbol X$ 的每一行是一个样本，每一列是一种特征。对于特征集合 $\boldsymbol X$ ，预测值可以通过矩$\widehat y \in \mathbb{R}^{n}$ 阵-向量乘法表示为：

$$\widehat y = \boldsymbol X \boldsymbol w + b$$

  具体过程是给定训练数据特征 $\boldsymbol X$ 和对应的已知目标 $y$，线性回归的目标是找到一组权重向量 $\boldsymbol w$ 和偏置 $b$。当给定从 $\boldsymbol X$ 的同分布中取样的新样本特征时，找到的 $\boldsymbol w$ 和$b$能够使得新样本预测的 $\widehat y$ 与 实际的 $y$ 之间的误差尽可能小。

  在我们开始寻找最好的模型参数model parameters的$\boldsymbol w$ 和 $b$ 之前，我们还需要两个东西：

1. 一种模型质量的度量方式；
2. 一种能够更新模型以提高模型预测质量的方法。

2.损失函数

  回归问题中最常用的损失函数是平方误差函数。当样本 $i$ 的预测值为 $\widehat{y}^{(i)}$，其相应的真实标签为 $y ^{(i)}$ 时，平方误差可以定义为以下公式：

$$l^{(i)}(\boldsymbol{w}, b) = \dfrac{1}{2} \left(\widehat{y}^{(i)} - y^{(i)}\right)^{2}$$

  常数 $\dfrac{1}{2}$ 不会带来本质的差别，但这样在形式上稍微简单一些，表现为当我们对损失函数求导后常数系数为 $1$ 。由于训练数据集并不受我们控制，所以经验误差只是关于模型参数的函数。

  由于平方误差函数中的二次方项，估计值 $\widehat{y}^{(i)}$ 和观测值 $y ^{(i)}$ 之间较大的差异将贡献更大的损失，即 $l$ 的值更大。为了度量模型在整个数据集上的质量，我们需计算在训练集 $n$ 个样本上的损失均值（也等价于求和）。

$$L(\boldsymbol{w}, b) = \dfrac{1}{n} \sum_{i=1}^{n} l^{(i)}(\boldsymbol{w}, b) = \dfrac{1}{2} \dfrac{1}{n} \sum_{i=1}^{n} \left(\widehat{y}^{(i)} - y^{(i)}\right)^{2} \\ \\ = \dfrac{1}{2n} \sum_{i=1}^{n}\left(\boldsymbol w^\mathrm{T} \boldsymbol x^{(i)} + b - y^{(i)}\right)^{2} = \dfrac{1}{2n} \left\|\boldsymbol{Xw} + b - \boldsymbol{y}\right\|^{2}$$

  在训练模型时，我们希望寻找一组参数 $\left(\boldsymbol{w}^*, b^*\right)$，这组参数能最小化在所有训练样本上的总损失。如下式：

$$\boldsymbol{w}^*, b^* = \mathop{argmin}\limits_{\boldsymbol{w}, b} L(\boldsymbol{w}, b)$$

3.解析解

  线性回归是一个很简单的优化问题，而线性回归的解可以用一个公式简单地表达出来，也就是其有显式解，这类解叫做解析解analytical solution。

  针对 $\boldsymbol {Xw} + b$ 式子，将原 $\boldsymbol{X}$ 后面加一列1变为新的 $\boldsymbol{X}$ ： $\boldsymbol{X} \gets [\boldsymbol{X}, 1]$；将原 $\boldsymbol w$ 与 $b$ 合并成新的 $\boldsymbol w$ ：$\boldsymbol{w} \gets \begin{bmatrix} \boldsymbol{w} \\ b \end{bmatrix}$ 。即 $L(\boldsymbol{w}, b) = \dfrac{1}{2n} \left\|\boldsymbol{Xw} + b - \boldsymbol{y}\right\|^2 = \dfrac{1}{2n} \left\|\boldsymbol{Xw} - \boldsymbol{y}\right\|^{2}$。

  我们将损失函数 $L(\boldsymbol w, b)$ 关于 $\boldsymbol w$ 求偏导，并将改导数值设为0，即可得到解析解：

$$\dfrac{\partial{L(\boldsymbol{w}, b)}}{\partial{\boldsymbol w}} = \dfrac{1}{n}(\boldsymbol{Xw} - \boldsymbol{y})^\mathrm{T}\boldsymbol{X} = 0 \\ \Leftrightarrow \boldsymbol{X}^\mathrm{T} \boldsymbol{w}^\mathrm{T} \boldsymbol{X} = \boldsymbol{y}^\mathrm{T} \boldsymbol{X} \\ \Leftrightarrow \boldsymbol{X}^\mathrm{T} \boldsymbol{w} \boldsymbol{X} = \boldsymbol{X}^\mathrm{T} \boldsymbol{y} \\ \Leftrightarrow \boldsymbol{w} = \left(\boldsymbol{X}^\mathrm{T}\right)^\mathrm{-1} \boldsymbol{X}^\mathrm{T} \boldsymbol{y} \left(\boldsymbol{X}\right)^\mathrm{-1} = \left(\boldsymbol{X}^\mathrm{T} \boldsymbol{X}\right)^\mathrm{-1} \boldsymbol{X}^\mathrm{T} \boldsymbol{y}$$

4.小批量随机梯度下降

  除了线性回归这样简单的模型外，其他模型大部分是得不到解析解的，而且在很多时候，那些难以得到解析解的模型效果更好，因此，弄清楚如何训练这些难以优化的模型是非常重要的。

  这里采用的是梯度下降gradient descent的方法，这种方法几乎可以优化所有深度学习模型。它通过不断地在损失函数递减的方向上更新参数来降低误差。

  梯度下降最简单的用法是计算损失函数（即数据集中所有样本的损失均值）关于模型参数的导数（在这里也可以称为梯度）。但实际中的执行可能会非常慢：因为在每一次更新参数之前，我们必须遍历整个数据集。因此，我们通常会在每次需要计算更新的时候随机抽取一小批样本，这种变体就叫做小批量随机梯度下降minibatch stochastic gradient descent。

  在每次迭代中，我们首先随机抽样一个小批量 $\mathcal B$ ，它是由固定数量的训练样本组成的。然后，我们计算小批量的平均损失关于模型参数的导数（也可以称为梯度）。最后，我们将梯度乘以一个预先确定的正数 $\eta$，并从当前参数的值中减掉。算法的步骤为：（1）初始化模型参数的值，如随机初始化 $\boldsymbol{w_0}$ 和 $b_0$ 。 （2）从数据集中随机抽取小批量样本且在负梯度的方向上更新参数，并不断迭代这一步骤。

  对于平方损失和仿射变换，我们可以明确地写成如下形式:

$$\boldsymbol{w_t} \gets \boldsymbol{w_{t-1}} - \dfrac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}\dfrac{\partial}{\partial \boldsymbol{w_{t-1}}} l^{(i)}(\boldsymbol{w_{t-1}}, b) \\ = \boldsymbol{w_{t-1}} - \dfrac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}\dfrac{\partial}{\partial \boldsymbol{w_{t-1}}} \dfrac{1}{2} \left(\boldsymbol w_{t-1}^\mathrm{T} \boldsymbol x^{(i)} + b - y^{(i)}\right)^{2} \\ = \boldsymbol{w_{t-1}} - \dfrac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \boldsymbol{x^{(i)}} \left(\boldsymbol w_{t-1}^\mathrm{T} \boldsymbol x^{(i)} + b - y^{(i)}\right)$$

$$b \gets b_{t-1} - \dfrac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \dfrac{\partial}{\partial b_{t-1}} l^{(i)}(\boldsymbol{w}, b_{t-1}) \\ = b_{t-1} - \dfrac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \dfrac{\partial}{\partial b_{t-1}} \dfrac{1}{2} \left(\boldsymbol w^\mathrm{T} \boldsymbol x^{(i)} + b_{t-1} - y^{(i)}\right)^{2} \\ = b_{t-1} - \dfrac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \left(\boldsymbol{w}^\mathrm{T} \boldsymbol x^{(i)} + b_{t-1} - y^{(i)}\right)$$

  公式中的 $\boldsymbol{w}$ 是权重向量， $\boldsymbol{x}$ 是特征向量， $|\mathcal{B}|$ 是每个小批量中的样本数（即批量大小batch size），$\eta$ 是学习率learning rate。

  调参hyperparameter tuning是选择超参数的过程。超参数通常是我们根据训练迭代结果来调整的，而训练迭代结果是在独立的验证数据集validation dataset上评估得到的。

  在训练了预先确定的若干迭代次数后（或者直到满足某些其他停止条件后），我们记录下模型参数的估计值，表示为 $\widehat{\boldsymbol w}$，$\widehat{b}$。但是，即使我们的函数确实是线性的且无噪声，这些估计值也不会使损失函数真正地达到最小值。因为算法会使得损失向最小值缓慢收敛，但却不能在有限的步数内非常精确地达到最小值。

  线性回归恰好是一个在整个域中只有一个最小值的学习问题。但是对于像深度神经网络这样复杂的模型来说，损失平面上通常包含多个最小值。幸运的是，出于某种原因，深度学习实践者很少会去花费大力气寻找这样一组参数，使得在训练集上的损失达到最小。事实上，更难做到的是找到一组参数，这组参数能够在我们从未见过的数据上实现较低的损失，这一挑战被称为泛化generalization。

  给定学习到的线性回归模型 $\widehat{\boldsymbol w}^\mathrm{T} \boldsymbol x + \widehat{b}$，现在我们可以通过给定的房屋面积 $x_1$ 和房龄 $x_2$ 来估计一个未包含在训练数据中的新房屋价格。给定特征估计目标的过程通常称为预测prediction或推断inference。

二、矢量化加速

  在训练我们的模型时，我们经常希望能够同时处理整个小批量的样本。为了实现这一点，需要我们对计算进行矢量化，从而利用线性代数库，而不是在Python中编写开销高昂的for循环。

  由于在沐神的书中将频繁地进行运行时间的基准测试，所以定义一个计时器。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

import time
import numpy as np


class Timer:
    """记录多次运行时间。"""

    def __init__(self):
        self.times = []
        self.start()

    def start(self):
        """启动计时器。"""
        self.tik = time.time()

    def stop(self):
        """停止计时器并将时间记录在列表中。"""
        self.times.append(time.time() - self.tik)
        return self.times[-1]

    def avg(self):
        """返回平均时间。"""
        return sum(self.times) / len(self.times)

    def sum(self):
        """返回时间总和。"""
        return sum(self.times)

    def cumsum(self):
        """返回累计时间。"""
        return np.array(self.times).cumsum().tolist()

  下面对两个全1的1000维向量，分别用for遍历的方法和使用重载的 + 运算符来计算按元素的和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14

n = 10000
a = torch.ones(n)
b = torch.ones(n)
timer = Timer()
# 用for遍历
c = torch.zeros(n)
timer.start()
for i in range(n):
    c[i] = a[i] + b[i]
print(f'{timer.stop():.5f} sec')
# 用重载运算符
timer.start()
d = a + b
print(f'{timer.stop():.5f} sec')

运行结果：

  可以看到速度天壤之别。

三、正态分布与平方损失

  接下来，我们通过对噪声分布的假设来解读平方损失目标函数。

  正态分布normal distribution和线性回归之间的关系很密切，学过概率的都知道，若随机变量 $x$ 具有均值 $\mu$ 和方差 $\sigma^{2}$（标准差 $\sigma$），其正态分布概率密度函数如下：

$$p(x) = \dfrac{1}{\sqrt{2 \pi \sigma^{2}}}exp\left(-\dfrac{1}{2\sigma^{2}} (x-\mu)^{2}\right)$$

  下面在python中定义一个计算正态分布的函数

1
2
3

def normal(x, mu, sigma):
    p = 1 / math.sqrt(2 * math.pi * sigma ** 2)
    return p * np.exp(-0.5 / sigma ** 2 * (x - mu) ** 2)

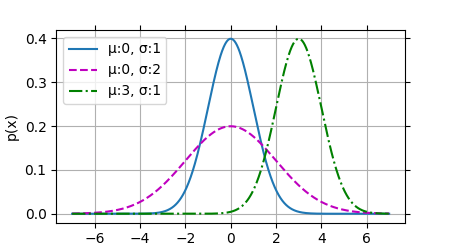
  然后可视化正态分布：

1
2
3
4
5
6
7

# 再次使用numpy进行可视化
x = np.arange(-7, 7, 0.01)

# 均值和标准差对
params = [(0, 1), (0, 2), (3, 1)]
plot(x, [normal(x, mu, sigma) for mu, sigma in params], xlabel='x', ylabel='p(x)', figsize=(4.5, 2.5),
     legend=[f'{chr(956)}:{mu}, {chr(963)}:{sigma}' for mu, sigma in params])

运行结果：

  就像我们所看到的，改变均值会产生沿 $x$ 轴的偏移，增加方差将会分散分布、降低其峰值。

  均方误差损失函数（简称均方损失）可以用于线性回归的一个原因是：我们假设了观测中包含噪声，其中噪声服从正态分布。噪声正态分布如下式:

$$y = \boldsymbol{w}^{\mathrm{T}} \boldsymbol{x} + b + \epsilon \quad where \quad \epsilon \sim \mathcal{N}\left(0,\sigma^{2}\right)$$

  因此，我们现在可以写出通过给定的 $\boldsymbol{x}$ 观测到特定 $y$ 的可能性likelihood：

$$P(y|\boldsymbol{x}) = \dfrac{1}{\sqrt{2 \pi \sigma^{2}}}exp\left(-\dfrac{1}{2\sigma^{2}} \left(y - \boldsymbol{w}^{\mathrm{T}} \boldsymbol{x} -b\right)^{2}\right)$$

  现在，根据最大似然估计法，参数 $\boldsymbol w$ 和 $b$ 的最优值是使整个数据集的可能性最大的值：

$$P(\boldsymbol{y}|\boldsymbol{X}) = \prod_{i=1}^{n} P\left(y^{(i)}|\boldsymbol{x}^{(i)}\right)$$

  根据最大似然估计法选择的估计量称为最大似然估计量。 虽然使许多指数函数的乘积最大化看起来很困难，但是我们可以在不改变目标的前提下，通过最大化似然对数来简化。 由于历史原因，优化通常是说最小化而不是最大化。我们可以改为最小化负对数似然 $−\ln P(\boldsymbol{y}|\boldsymbol{X})$。由此可以得到的数学公式是：

$$−\ln P(\boldsymbol{y}|\boldsymbol{X}) = −\ln \left(\dfrac{1}{\sqrt{2 \pi \sigma^{2}}}exp\left(-\dfrac{1}{2\sigma^{2}} \left(y^{(i)} - \boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}^{(i)} -b\right)^{2}\right) \right) \\ = \sum_{i=1}^{n} \dfrac{1}{2} \ln\left(2\pi\sigma^{2}\right) + \dfrac{1}{2\sigma^{2}} \left(y^{(i)} - \boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}^{(i)} -b\right)^{2}$$

  现在我们只需要假设 $\sigma$ 是某个固定常数就可以忽略第一项，因为第一项不依赖于 $\boldsymbol{w}$ 和 $b$。现在第二项除了常数 $\frac{1}{2\sigma^{2}}$ 外，其余部分和前面介绍的平方误差损失是一样的。 幸运的是，上面式子的解并不依赖于 $\sigma$。因此，在正态（高斯）噪声的假设下，最小化均方误差等价于对线性模型的最大似然估计。

四、从线性回归到深度网络

  我们可以将线性回归模型视为仅由单个人工神经元组成的神经网络，或称为单层神经网络。